Du befinner dig vid A och har ett avståndsinstrument av något slag, kanske rentutav ett laserinstrument.
Avstånden A-B och A-C är således lätta att fastställa.

Du vill veta avståndet B-C men kan av vissa skäl inte gå fram i terrängen.
Hur gör du?

Den som har varit med förut mäter naturligtvis vinkeln mella B och C och tillämpar sedan sina solida kunskaper i geometri.

Om du har glömt din geometri så har vi ju den gamla goda streckformeln att ta till.
Mer om den längre ned.

Här ser vi streckskalan i en kikare m/1928. I modernare militära kikare finns det streckskala även på höjden.

Vinkelmätning med kikare förekommer bland annat vid eldledning av artilleri- och granatkastarförband.

Äntligen kan vi nu tillämpa den kära gamla streckformeln.

Vinkeln i streck gånger avståndet i kilometer är lika med fronten i meter

I vårt fall blir det
350· 0,6 = 210

Sträckan B-C är alltså 210 meter

Precisionen är inte 100%-ig eftersom vi inte tar hänsyn till sträckan A-C men för fältbruk är noggrannheten oftast tillräcklig.

....

Det finns flera metoder för att mäta vinklar i fält. Här ser vi ett mycket enkelt hjälpmedel i form av en "skjutregelsticka" för kulspruta m/1914.
Håll stickan på rak arm och syfta över streckskalan som omspänner 300¯.
Noggrannheten blir tillräcklig för fältbruk.

Till nöds kan man syfta över knogarna på rak arm.
Mycket grovt räknat antas en knoge vara 30¯ och tre knogar 100¯ vilket ger tillräcklig noggrannhet för till exempel eldledning av artilleri och granatkastare.
(Stämmer exakt om tre knogar=60 mm och avstånd öga till knogar=0,6 m)

Där två räta linjer möts bildas en vinkel (och en yttervinkel).
Vinklar mäts till exempel i grader (°).
Avsätts vinklar från medelpunkten (origo) i en cirkel så går det 360° på ett fullt cirkelvarv.
Detaljerna kring detta kan utforskas bl a på Wikipedia och Google.

Ett fjärdedels cirkelvarv omfattar således 90° vilket också kallas för en rät vinkel.

En rät vinkel markeras grafiskt som visas med rött i vidstående bild.

En rät linje mellan två punkter på en cirkelbåge genom origo är cirkelns diameter (D). En rät linje från origo till en punkt på cirkelbågen är en radie (r). Således är 2r=D.

Här ovan ses alltså strängt taget två diametrar och fyra radier.

Nu kommer vi till det magiska talet pi (π)
Redan för ett par tusen år sedan förstod man att cirkelns omkrets delad med diametern var av avgörande betydelse för geometriska beräkningar. Archimedes förfinade teorierna och så var talet 3,14 etablerat. Egentligen är antalet decimaler oändligt. Ibland använder man t ex 3,1416.

En cirkels omkrets är pi· 2· r,alltså ≈ 6,283 radier

Cirkelns yta är pi· r· r

Vill du veta mer om detta så hänvisas du återigen till Wikipedia och Google.

360° är egentligen ett konstigt vinkelmått, svårt att hantera matematiskt. Var kom 360 ifrån?

Ett bättre vinkelmått är radianer (rad). Anta att vi tar en radie och kröker ihop den och placerar den på omkretsen. Den omsluts av centrumvinkeln 1 rad.
Radianer är den härledda SI-enheten för vinkelmått.

Dela upp vinkeln 1 rad i ettusen delar så har vi fått milliradianer (mrad), närmare bestämt 1000· 2· pi ·≈ 6283 mrad på ett helt cirkelvarv. Nu har vi fått precision i vinkelmätandet. Kalkylprogrammet Excel har milliradianer som bas.

Nu börjar det likna nå't! Vi som har varit med ett tag vet ju att vi har använt vinkelmåttet streck i militära sammanhang. 6283 mrad har förenklats till 6300 streck (¯). Avstånd kan vi mäta med diverse instrument men "fronten" är svår att mäta på avstånd och det har vi behov av bland annat för att kunna leda artilleri- och granatkastareld. Den gyllene streckformeln lyder:
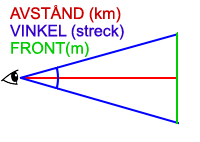
"Vinkeln i streck gånger avståndet i kilometer är lika med fronten i meter"

Inom NATO har man länge tillämpat vinkelmåttet mils som även det är en förenkling av millirad. Numer tilläpas mils även i Sverige. 6400 mils är matematiskt mer hanterbart än både 6300 streck och 360 grader.

Nu kan man undra hur länge det dröjer innan alla kikare och riktinstrument med mera har ändrats till mils. Kompasser och mätskivor måste nyanskaffas. Mycket väsen för lite ull kan man tycka.